BNF Converter Tutorial

Aarne Ranta

BNFC = BNF Converter

BNF = Backus-Naur Form (also known as Context-Free Grammars).

BNF is the standard format for the specification and documentation of programming languages.

BNFC makes BNF usable for implementation as well.

BNFC is a high-level front end to traditional implementation formats (in the style of Lex and YACC): "BNFC is a compiler compiler compiler"

BNFC saves 90% of source code writing in a typical compiler front end.

BNFC can be used for projects carried out in Agda, C, C++, Haskell, Java, OCaml.

What BNFC can be used for

Strongest case: when designing and implementing a new programming language

BNFC also scales up to legacy programming languages

How to obtain BNFC

BNFC homepage: http://bnfc.digitalgrammars.com/

You can obtain

If you are using Debian or Ubuntu Linux, you can obtain BNFC with their package system (but it is a slightly older version).

For the binaries, it is enough to download them and put into a place where you can find executables (such as /usr/local/bin on Unix-like platforms).

Working with BNFC sources

If you choose the source package, you need the GHC Haskell Compiler. With GHC in place, just unpack the sources, cd to BNFC, and type make.

If you want to contribute to BNFC, make sure you use the latest git version: give the command

git clone https://github.com/BNFC/bnfc.git

BNFC is licensed under the BSD 3-clause license.

Calling BNFC

When you have BNFC in place (i.e. on your path), you can all it by

    bnfc

This gives you a list of available options. The most common choices are:

    bnfc -m --c       FILE.cf      # to generate C
    bnfc -m --cpp     FILE.cf      # to generate C++ with STL
    bnfc -m --java    FILE.cf      # to generate Java ≥ 1.5
    bnfc -m --haskell FILE.cf      # to generate Haskell

The -m flag makes BNFC to generate a Makefile. This means that, after running bnfc, you can create an executable parser by

    make

Let us now create our first application from a BNFC source file.

My first compiler: calculator

We start with everyone's favourite: the desktop calculator.

To make it the simplest possible, we restrict ourselves to integers, with addition, subtraction, multiplication, and (lossy) division.

The input language is defined with the following BNFC grammar.

    EAdd. Exp  ::= Exp  "+" Exp1 ;
    ESub. Exp  ::= Exp  "-" Exp1 ;
    EMul. Exp1 ::= Exp1 "*" Exp2 ;
    EDiv. Exp1 ::= Exp1 "/" Exp2 ;
    EInt. Exp2 ::= Integer ;

    coercions Exp 2 ;

Copy this code into a file called Calc.cf.

We return to the details of the notation after trying this out in BNFC.

Compiling the compiler in Java

If you want to work in Haskell, C, or C++, skip a few sections now.

Assuming you want to work in Java, do the following:

    bnfc -m --java Calc.cf
    make

If everything goes fine, this will create a parser test class, which you can try out in the following way:

    echo "23 + 4 * 70" | java Calc/Test

    Parse Succesful!
    [Abstract Syntax]
    (EAdd (EInt 23) (EMul (EInt 4) (EInt 70)))
    [Linearized Tree]
    23 + 4 * 70

However, this will probably not work at first time: you will have to install some more software and set a classpath.

Putting parser and lexer tools for Java in place

When you called BNFC, you saw it generate lots of files. Most of them were .java files, but there were two special ones:

You will need to download and install both of the required tools:

It is safest to take the named versions, even if there were newer ones available.

In addition to these, you of course need the Java compiler and runtime environment available from Sun.

Cup comes as a package of java and class files. Just unpack it in some directory, e.g. /usr/local/java/Cup.

JLex is just one Java file. Put it in some directory, e.g. /usr/local/java/JLex. Compile it with javac Main.java in that directory.

Setting the Java class path

After installing Cup and JLex, compiling with

    bnfc -m --java Calc.cf
    make

will probably still fail, with a message saying that a class was not found. Fix this by

    export CLASSPATH=.:/usr/local/java/Cup:/usr/local/java

provided you put Cup and JLex in places as specified above. Notice also the inclusion of the current working directory (.).

If export doesn't work: in some Unix shells, the CLASSPATH variable is set with the command

    setenv CLASSPATH .:/usr/local/java/Cup:/usr/local/java

Now you will hopefully be able to compile and run the compiler.

Compiling the compiler in Haskell

Assuming you want to work in Haskell, do the following:

    bnfc -m --haskell Calc.cf
    make

If everything goes fine, this will create a parser test executable, which you can try out in the following way:

    echo "23 + 4 * 70" | ./TestCalc

    Parse Successful!
    [Abstract Syntax]
    EAdd (EInt 23) (EMul (EInt 4) (EInt 70))
    [Linearized tree]
    23 + 4 * 70

The tools that you need to have installed are

Compiling the compiler in C and C++

Assuming you want to work in C or C++, do the following:

    bnfc -m -c    Calc.cf     # in C
    bnfc -m --cpp Calc.cf     # in C++
    make

If everything goes fine, this will create a parser test executable, which you can try out in the following way:

    echo "23 + 4 * 70" | ./testCalc

    Parse Successful!
    [Abstract Syntax]
    EAdd (EInt 23) (EMul (EInt 4) (EInt 70))
    [Linearized tree]
    23 + 4 * 70

The tools that you need to have installed are

The most common source of problems is wrong version of Bison. If the test program always results in error: parse error, check the version with bison --version.

What there is in a BNFC file

A BNFC source file is a sequence of rules, where most rules have the format

    LABEL . VALUE_CATEGORY ::= PRODUCTION ;

The LABEL and VALUE_CATEGORY are identifiers (without quotes).

The PRODUCTION is a sequence of

The rule has the following semantics:

Types of trees are the categories of the grammar. Tree labels are the constructors of those categories.

Common problems with identifiers

All categories and constructors should

These three conditions guarantee that the grammar will work on all platforms.

Example of a tree

In the examples above, the string

    23 + 4 * 70

was compiled into a tree displayed as follows:

    EAdd (EInt 23) (EMul (EInt 4) (EInt 70))

This is just a handy (machine-readable!) notation for the "real" tree

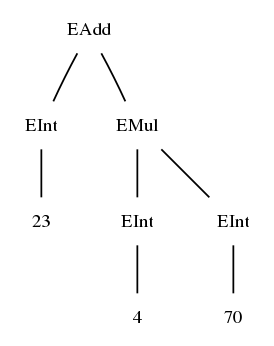
Example tree showing precedence levels

(You may also notice that it is exactly the notation Haskell programmers use for specifying trees.)

Precedence levels

How does BNFC know that addition is above multiplication? I.e., why isn't the tree

    EMul (EAdd (EInt 23) (EInt 4)) (EInt 70)

This is due to the fact that multiplication expressions are given higher precedence.

The nonterminal Exp has precedence level 0 (actually, we could write Exp0 to mean the same), Exp1 has precedence level 1, etc.

The rule

    EAdd. Exp  ::= Exp  "+" Exp1 ;

says: EAdd forms an expression of level 0 from an expression of level 0 on the left of + and of level 1 on the right.

Likewise, the rule

    EMul. Exp1 ::= Exp1 "*" Exp2 ;

says: EMul form an expression of level 1 from an expression of level 1 on the left of * and of level 2 on the right.

Semantics of precedence levels

An expression of higher level can always be used on lower levels as well.

An expression of any level can be lifted to the highest level by putting it in parentheses.

The rule coercions Exp 2 says that 2 is the highest level for Exp.

All precedence variants of a nonterminal denote the same type.

This means that a type-correct tree remains type-correct, if a subtree of category Expi is changed into a subtree of Expj.

The deeper semantics of precedence levels: dummy labels

BNFC permits a dummy label, which does not construct a new tree but just returns the old one (which must be of same type):

    _. Exp2 ::= "(" Exp ")" ;

The rule (coercions Exp 2) is a shorthand for a group of dummy rules:

    _. Exp  ::= Exp1 ;
    _. Exp1 ::= Exp2 ;
    _. Exp2 ::= "(" Exp ")" ;

Compiler components

BNFC generates the following components:

The first three belong to a compiler front end, analysing the source code.

The compiler back end can either

Abstract syntax

The hub of a modern compiler:

In the middle of the front end and back end, there is manipulation of abstract syntax, such as type checking and optimizations.

Abstract syntax representations in programming languages (as generated by BNFC):

Abstract syntax in Haskell

This is the most straightforward, so we start from it.

For every type in the grammar, a data definition is produced:

    data Exp =
       EAdd Exp Exp
     | ESub Exp Exp
     | EMul Exp Exp
     | EDiv Exp Exp
     | EInt Integer
      deriving (Eq,Ord,Show)

The deriving part says that the type Exp has equality and order predicates, and its objects can be shown as strings.

The complete code is in the file AbsCalc.hs.

An interpreter in Haskell: the tree traversal

We write a program that parses an arithmetic expression and returns a numeric value.

Here is the tree traversal: pattern matching on the type Exp.

    module Interpreter where

    import AbsCalc

    interpret :: Exp -> Integer
    interpret x = case x of
      EAdd exp0 exp  -> interpret exp0 + interpret exp
      ESub exp0 exp  -> interpret exp0 - interpret exp
      EMul exp0 exp  -> interpret exp0 * interpret exp
      EDiv exp0 exp  -> interpret exp0 `div` interpret exp
      EInt n  -> n

The complete code is in the file Interpreter.hs.

An interpreter in Haskell: the main function

We write a module reading string input calling Interpreter.interpret.

The string is first lexed and parsed. The file Interpret.hs. is modified from TestCalc.hs.

    module Main where

    import LexCalc
    import ParCalc
    import AbsCalc
    import Interpreter

    import ErrM

    main = do
      interact calc
      putStrLn ""

    calc s =
      let Ok e = pExp (myLexer s)
      in show (interpret e)

Skeleton for tree processing in Haskell

Recursive functions making case analysis on trees is used in almost all components of the compiler.

BNFC gives a template for this, the skeleton file SkelCalc.hs, with a dummy tree processing function:

    transExp :: Exp -> Result
    transExp x = case x of
      EAdd exp0 exp  -> failure x
      ESub exp0 exp  -> failure x
      EMul exp0 exp  -> failure x
      EDiv exp0 exp  -> failure x
      EInt n  -> failure x

    type Result = Err String

    failure :: Show a => a -> Result
    failure x = Bad $ "Undefined case: " ++ show x

Compiling and running the interpreter in Haskell

Compile with GHC:

    ghc --make Interpret.hs

Run on command-line input:

    echo "1 + 2 * 3" | ./Interpret
    7

Run on file input (ex1.calc):

    ./Interpret < ex1.calc
    9102

Now, if you are not working in Java, C, or C++, you can take a long leap.

Abstract syntax in Java

For each category in the grammar, an abstract base class is generated.

For each constructor of the category, a class extending the base class.

This means quite a few files, put into the subdirectory Calc/Absyn/:

    Calc/Absyn/EAdd.java
    Calc/Absyn/EDiv.java
    Calc/Absyn/EInt.java
    Calc/Absyn/EMul.java
    Calc/Absyn/ESub.java
    Calc/Absyn/Exp.java

Inside the abstract syntax Java classes

    public abstract class Exp implements java.io.Serializable {

    // some code that we explain later
    }

    public class EAdd extends Exp {
      public final Exp exp_1, exp_2;
      public EAdd(Exp p1, Exp p2) { exp_1 = p1; exp_2 = p2; }

    // some more code that we explain later
    }

    /* the same for ESub, EMul, EDiv */

    public class EInt extends Exp {
      public final Integer integer_;
      public EInt(Integer p1) { integer_ = p1; }
    }

Tree processing in Java: the Visitor

For each category in the grammar, a Visitor interface and an abstract accept method are generated.

For each constructor of the category, an accept method overriding the abstract accept.

    public abstract class Exp implements java.io.Serializable {
      public abstract <R,A> R accept(Exp.Visitor<R,A> v, A arg);
      public interface Visitor <R,A> {
        public R visit(Calc.Absyn.EAdd p, A arg);
        public R visit(Calc.Absyn.ESub p, A arg);
        public R visit(Calc.Absyn.EMul p, A arg);
        public R visit(Calc.Absyn.EDiv p, A arg);
        public R visit(Calc.Absyn.EInt p, A arg);
      }
    }

    public class EAdd extends Exp {
      public final Exp exp_1, exp_2;
      public EAdd(Exp p1, Exp p2) { exp_1 = p1; exp_2 = p2; }

      public <R,A> R accept(Calc.Absyn.Exp.Visitor<R,A> v, A arg)
      {
        return v.visit(this, arg);
      }

The meaning of the Java Visitor

interface Exp.Visitor <R,A>: collection of methods for

R accept(Exp.Visitor<R,A> v, A arg): a method for using a visitor and returning a value

Recursive tree traversal:

An interpreter in Java: tree processing

The program uses the visitor skeleton as basis, with Integer as return type and Object as argument type (a dummy argument):

    private static class Calculator implements Exp.Visitor<Integer,Object> {

      public Integer visit(Calc.Absyn.EAdd p,Object o)
      {
        Integer a = p.exp_1.accept(this, null);
        Integer b = p.exp_2.accept(this, null);
        return a + b;
      }

      /* correspondingly for ESub, EMul, EDiv */

      public Integer visit(Calc.Absyn.EInt p, Object o)
      {
        return p.integer_;
      }
    }

Java code around tree processing

The complete code is in the file Interpreter.java:

    package Calc;
    import Calc.Absyn.*;

    public class Interpreter {

      public static Integer interpret(Exp e)
      {
    Exp exp = (Exp)e ;
    return interpretExp(exp, null) ;
      }

      private static Integer interpretExp(Exp e, Object o)
      {
    return e.accept(new Calculator(), null) ;
      }

      private static class Calculator implements Exp.Visitor<Integer,Object> {

      // the tree traversal: see previous section
      }
    }

Tree processing in Java: the skeleton

You can use the BNFC-generated file Calc/VisitSkel.java as a template for writing your own visitor applications:

    public class VisitSkel {
      public class ExpVisitor<R,A> implements Exp.Visitor<R,A> {
        public R visit(Calc.Absyn.EAdd p, A arg)
        {
          /* Code For EAdd Goes Here */
          p.exp_1.accept(new ExpVisitor<R,A>(), arg);
          p.exp_2.accept(new ExpVisitor<R,A>(), arg);
          return null;
        }

        public R visit(Calc.Absyn.EInt p, A arg)
        {
          /* Code For EInt Goes Here */
          //p.integer_;
          return null;
        }
      }
    }

An interpreter in Java: main class

The program Interpret.java modifies the BNFC-generated Test.java, by changing the tree output to a call of the interpreter:

    public class Interpret {
      public static void main(String args[]) throws Exception
      {
        Yylex l  = new Yylex(System.in) ;
        parser p = new parser(l) ;
        Calc.Absyn.Exp parse_tree = p.pExp() ;
        System.out.println(Interpreter.interpret(parse_tree)) ;
      }
    }

(We have omitted error handling.)

Compiling and running the interpreter in Java

Compile with javac:

    javac Calc/Interpret.java

Run on command-line input:

    echo "1 + 2 * 3" | java Calc/Interpret
    7

Run on file input:

    java Calc/Interpret < ex1.calc
    9102

Abstract syntax in C

Simpler than in Java but more complex than in Haskell.

For every type in the grammar, a structure containing a tagged union of structures is created:

    struct Exp_ {
      enum { is_EAdd, is_ESub, is_EMul, is_EDiv, is_EInt } kind;
      union {
        struct { Exp exp_1, exp_2; } eadd_;
        struct { Exp exp_1, exp_2; } esub_;
        struct { Exp exp_1, exp_2; } emul_;
        struct { Exp exp_1, exp_2; } ediv_;
        struct { Integer integer_; } eint_;
      } u;
    };

    typedef struct Exp_ *Exp ;

    Exp make_EAdd(Exp p0, Exp p1);
    Exp make_ESub(Exp p0, Exp p1);
    Exp make_EMul(Exp p0, Exp p1);
    Exp make_EDiv(Exp p0, Exp p1);
    Exp make_EInt(Integer p0);

The complete code is in the files Absyn.h and Absyn.c.

An interpreter in C: tree traversal

We modify the skeleton (next section), changing the return type and the name of visitExp:

    int interpret(Exp _p_)
    {
      switch(_p_->kind)
      {
      case is_EAdd:
        return interpret(_p_->u.eadd_.exp_1) + interpret(_p_->u.eadd_.exp_2) ;
      case is_ESub:
        return interpret(_p_->u.eadd_.exp_1) - interpret(_p_->u.eadd_.exp_2) ;
      case is_EMul:
        return interpret(_p_->u.eadd_.exp_1) * interpret(_p_->u.eadd_.exp_2) ;
      case is_EDiv:
        return interpret(_p_->u.eadd_.exp_1) / interpret(_p_->u.eadd_.exp_2) ;
      case is_EInt:
        return _p_->u.eint_.integer_ ;
      }
    }

The complete code is in the files Interpreter.h and Interpreter.c.

Tree processing skeleton in C

The skeleton defines visit functions for all categories using case analysis over constructor tags.

    void visitInteger(Integer i);

    void visitExp(Exp _p_)
    {
      switch(_p_->kind)
      {
      case is_EAdd:
        /* Code for EAdd Goes Here */
        visitExp(_p_->u.eadd_.exp_1);
        visitExp(_p_->u.eadd_.exp_2);
        break;

      /* similarly for other binary ops */

      case is_EInt:
        /* Code for EInt Goes Here */
        visitInteger(_p_->u.eint_.integer_);
        break;
      }
    }

The complete code is in the files Skeleton.h and Skeleton.c.

An interpreter in C: main function

The string is first lexed and parsed.

    #include <stdio.h>
    #include <stdlib.h>
    #include "Parser.h"
    #include "Printer.h"
    #include "Absyn.h"
    #include "Interpreter.h"

    int main(int argc, char ** argv)
    {
      FILE *input;
      input = stdin;
      Exp parse_tree = pExp(input);
      if (parse_tree)
      {
        printf("%d\n", interpret(parse_tree));
        return 0;
      }
      return 1;
    }

The complete code is in the file Interpret.c, modified from the BNFC-generated Test.c.

Compiling and running the interpreter in C

Compile with GCC:

    gcc -c Interpreter.c Interpret.c
    gcc *.o -o interpret

Run on command-line input:

    echo "1 + 2 * 3" | ./interpret
    7

Run on file input:

    ./interpret < ex1.calc
    9102

A larger source language

We want to build a grammar of "C--", a fragment of C sufficient for parsing the following Fibonacci program:

    // a fibonacci function showing most features of the CMM language

    int mx ()
    {
      return 5000000 ;
    }

    int main ()
    {
      int lo ;
      int hi ;
      lo = 1 ;
      hi = lo ;
      printf("%d",lo) ;
      while (hi < mx()) {
        printf("%d",hi) ;
        hi = lo + hi ;
        lo = hi - lo ;
      }
    return 0 ;
    }

List categories

Lists are used everywhere in grammars. BNFC the category symbol [C] for a list of Cs.

Thus a program is a list of functions:

    Prog. Program ::= [Function] ;

A function has a list of declarations and a list of statements:

    Fun. Function ::= Type Ident "(" [Decl] ")" "{" [Stm] "}" ;

Terminators and separators

Lists have terminators and separators:

    terminator Function "" ;
    terminator Stm "" ;
    separator Decl "," ;

The empty terminator "" means the elements are just written next to each other.

A list can be forced to have at least one element:

    separator nonempty Ident "," ;

Abstract syntax for lists

Haskell: [C] is translated as [C]

Java 1.5: [C] is translated as java.util.LinkedList<C>

C++ with STL: [C] is translated as vector<C*>

C: [C] is translated as a struct implementing the linked list of C.

Comments

Comments are parts of source codes that the compiler ignores.

BNFC permits the definition of two kinds of comments: one-line and enclosed.

They are defined in the following ways for C--:

    comment "//" ;
    comment "/*" "*/" ;

Thus one-line comment definitions define the beginning of a comment, and enclosed comment definitions the beginning and the end.

Commends are resolved by the lexer, using a finite automaton. Therefore nested comments are not possible.

Complete grammar for C--

  comment "//" ;
  comment "/*" "*/" ;

  Prog. Program  ::= [Function] ;
  Fun.  Function ::= Type Ident "(" [Decl] ")" "{" [Stm] "}" ;
  Dec.  Decl     ::= Type [Ident] ;

  terminator Function "" ;
  terminator Stm "" ;
  separator  Decl "," ;
  separator  nonempty Ident "," ;

  SDecl.   Stm ::= Decl ";"  ;
  SExp.    Stm ::= Exp ";" ;
  SBlock.  Stm ::= "{" [Stm] "}" ;
  SWhile.  Stm ::= "while" "(" Exp ")" Stm ;
  SReturn. Stm ::= "return" Exp  ";" ;

  EAss.    Exp  ::= Ident "=" Exp ;
  ELt.     Exp1 ::= Exp2 "<" Exp2 ;
  EAdd.    Exp2 ::= Exp2 "+" Exp3 ;
  ESub.    Exp2 ::= Exp2 "-" Exp3 ;
  EMul.    Exp3 ::= Exp3 "*" Exp4 ;
  Call.    Exp4 ::= Ident "(" [Exp] ")" ;
  EVar.    Exp4 ::= Ident ;
  EStr.    Exp4 ::= String ;
  EInt.    Exp4 ::= Integer ;
  EDouble. Exp4 ::= Double ;

  coercions Exp 4 ;

  separator Exp "," ;

  TInt.    Type ::= "int" ;
  TDouble. Type ::= "double" ;

Built-in token types

These types are hard-coded and cannot be value types of rules:

Precise definitions are given in the LBNF report.

Token definitions

A grammar can define new token types by using regular expressions. Here is an example of the format:

    token CIdent (letter (letter | digit | '_')*) ;

See LBNF report for more information.

Remembering the position of a token

The position of a token can be passed to the syntax tree:

    position token CIdent (letter (letter | digit | '_')*) ;

See LBNF report for more information.

Common problems

Java: CLASSPATH, should contain ., Cup directory, JLex directory

C and C++: Bison version, should be ≥ 1.875

All grammars: conflicts. Use parser diagnosis tools to find and solve them!

Further reading

BNFC homepage: http://bnfc.digitalgrammars.com/

The LBNF report, covering the whole Labelled BNF grammar language used in BNFC:

Chalmers Programming Languages course notes: www.cs.chalmers.se/Cs/Grundutb/Kurser/progs/current/

Appel's book series Modern Compiler Implementation in ML/C/Java. BNFC generates abstract syntax representations as used in these books.

Dragon book: Aho, Lam, Sethi, Ullman, Compilers Principles, Techniques and Tools, 2007.